文章基本信息
- 标题:学習機構の解析に関する方法論的研究 (第2報告) 学習準備性 (点) の解析 (2)
- 作者:中嶽 治麿
- 期刊名称:教育心理学研究
- 印刷版ISSN:0021-5015
- 电子版ISSN:2186-3075
- 出版年度:1962
- 卷号:10
- 期号:1
- 页码:11-19,63
- DOI:10.5926/jjep1953.10.1_11
- 出版社:The Japanese Association of Educational Psychology
- 摘要:
ここでは, 学習準備点を構成する要素の抽出と, 準備点の構造を検討することに主眼をおいた。まず, 教材 (α) に対する学習準備点の構成要素を抽出する方法は次のようである。学習の準備に必要な要素を (Si, Si+1, …, Sj) と仮定すると, 教材 (α) の学習後に認められる (α) の達成度fα (s1, s2, …, sn) と, 各要素の理解の型 (s1, s2, …, sn) の関係は, 論理的には,(1)(2) 式のようになると考えられる。また, このような条件のもとでは,(4) 式の値は, Skが学習準備点の構成要素であれば, (mは準備点の構成要素の数) となり, 構成要素でないと, QK=0 となる。したがつて, これから, いちおう, 学習準備点の構成要素を,(4)(5) 式によつて抽出することができる。 しかし, 学習準備点は, このような簡単な構造をもつもののみではない。そこで, 上述のような構造は, 教材 (α) に関する学習準備点を構成する要素が, 1つでも理解できていない場合, 教材 (α) に対する学習効果はほとんど期待できないということから, 各要素はこの面で等 しい重さをもつているとみて, このような構造を, equal weight structureと名づけた。これに対して, unequal weight structure考え, これに, Or-structureとAnd-structureを取りあげた。前者は, 学習準備点の構成要素 (Sz+k1) の代わりに (Si+k2),((Si+k2) の代わりに (Si+k1)) をもつてくることができるというような構造をもつものであり, 後者は,(Si+k1) が十分に理解されていなくても,(Si'+k2) と共働して, ひとつの概念が成立しておればよいという構造をもつものである。 しかし, このAnd-structureは, equal weightstructureと, Or-structureの拡張と考えられるためにここでは, Or-structureをunequal weight structureの主要なものとして検討した。そうして, Or-structureに認められるOr-elementの性格を検討し,(11) 式のような方法で, これを抽出することを考えた。しかし, 学習準備点の構造というものは, このような単純なものばかりではない。そこで, いちおう, このような考えかたを拡張する方法や, 実際に学習準備点の構成要素を抽出する方法, さらに, この場合に考えなければならない問題などを5で考えた。
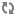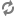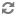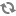 Loading...
Loading...
