文章基本信息
- 标题:学習機構の解析に関する方法論的研究: V 学習能力系列の解析 (2)
- 作者:中嶽 治麿
- 期刊名称:教育心理学研究
- 印刷版ISSN:0021-5015
- 电子版ISSN:2186-3075
- 出版年度:1962
- 卷号:10
- 期号:4
- 页码:193-204,250
- DOI:10.5926/jjep1953.10.4_193
- 出版社:The Japanese Association of Educational Psychology
- 摘要:
ここでは, 学習能力がより高まつていく方向に発展していく場合の系列のうち, 系列 (3) に示すような多重系列を, どのようにして抽出し評価するかという問題を, 主としてその能力に関する学習が終了した集団を対象とした学力検査の結果から, 能力の各発展段階に対する尺度性を仮定することによつて, 検討する方法を考えた。 まず, 目標 (G) に至るすべての相異なる最も簡単な構造をもつ単一系列を抽出し, これを互いに素な系列反応型とよぶことにした。次に, 互いに素な系列反応型をみると, 系列 (3-1) のような特定の性質によつて規定される構造をもつ系列 (完全多重系列) については, 系列内の各要素が1または0を特定の法則にしたがつてとつていることがわかる。(互いに素な系列反応型の構成要素であるときは1, そうでないときは0とする。) たとえば, 系列 (3-1) では, 能力 (Ai・j) が1をとる互いに素な系列反応型の数をR (Ai・j;k)(kは系列の長さ) とすると, 〓となる。また, 系列内の各要素間の関係〓を求めると, i=pのときは〓となる。このような特性に注目して完全多重系列を検討すると, その大部分は, 特定の条件のもとでは, 一意的に系列を抽出することができる。 また, 特定の性質によつて規定される構造をもたない (3-2) のような系列 (不完全多重系列) についても, 系列内の各要素が示す尺度性と, 上記特性とをあわせて検討することによつて, いちおう, いくつかの系列を抽出することが可能になる。 終りに, このようにして抽出された系列をどう評価するかを考えた。その方針は, 系列の太さと, 系列上の各要素が示す目標到達度である。系列の太さとは, その系列に沿つた能力の発展体系をもつている被検者が, 全体の何パーセントを占めているかをみたものであり, 目標到達度とは, 系列上の各要素について, そこに到達できたものの何パーセントが, 目標に到達できるかを示したものである。 こうすると, 比較的好ましい系列は, より太い系列で, 到達度の高い要素を含むものということになる。 しかし, このような能力の系列は, 被検者が受けた教育作用によつて, 大きく左右される。したがつて, どの' ような教育作用を受け, どのような特性をもつ集団が, 系列の抽出に用いられたかが大きい問題になる。このような問題を, 比較的さけることができるのは, より多くの標準的な被検者を対象とした学力検査結果を利用することであろうが, これについても, なお問題は残つている。しかし, 実際にはこのような手法を繰返すことによつて, だんだんにより好ましい学習能力系列が抽出され, これに基づいた, より有効な指導計画の設定が可能になるのではないかと考えられる。 〔追記〕この研究に関して, 名古屋大学教育学部, 白石教授のご指導を頂きました。ここで厚くお礼申しあげます。
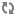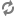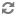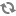 Loading...
Loading...
